In the previous article we saw how a transformer model can learn to execute a multi-step algorithm to sort lists of numbers. One drawback of this approach is that we need to devise the algorithm ourselves, and it is likely not the most efficient algorithm for sorting lists. Instead, it would be better if the model could learn its own highly efficient algorithm from scratch, having been shown only the expected inputs and outputs of the algorithm, just like this one:
The training code for this model can be found on GitHub.
How it Works
The previous model worked by generating the intermediate steps of bubble sort before generating the final sorted list. This approach is effective but slow, as bubble sort requires up to N2 steps to sort a list of length N, so up to N3 tokens are needed to output all the intermediate lists. This new model instead generates a sequence of blank tokens (specifically the 11 token) before producing the final sorted list, which means we do not need to provide the sorting algorithm ourselves. Also, the number of blank tokens generated is always the same: 49, which is equal to the maximum input length the model is trained on. This means that where the previous model would require over 117,000 tokens to sort the longest list, this model only requires 49!
This approach leads to a natural question: how can generating blank tokens help the model to sort a list? Clearly, the values of these tokens themselves are not helpful, as they are the same for all input lists. The secret lies inside the model, which generates internal key-value pairs from previous tokens as it runs. By adding a sequence of blank tokens before the final answer, the model is given a chance to perform more computation on the input list before producing the sorted output.
Attention Patterns
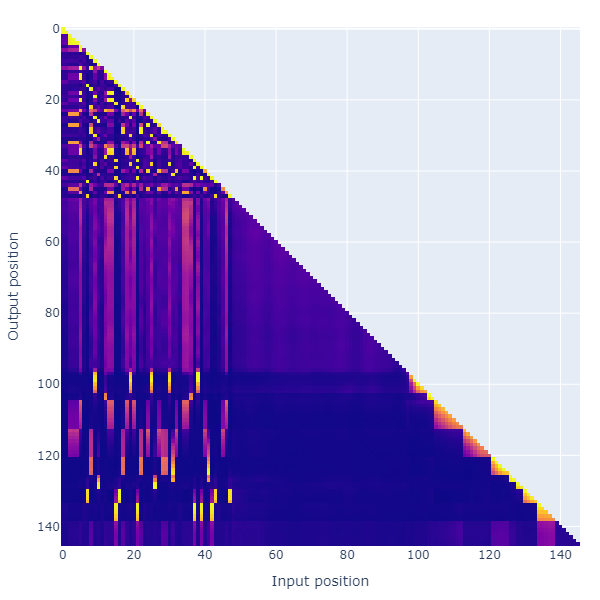
The above figure shows the attention patterns of the model as it runs. Each row of the plot corresponds to the attention weights being applied to all the tokens generated so far. At first it might look like the model only pays attention to the input and output lists,with the blank intermediate tokens having very low weight. However I find that if I mask out the intermediate tokens when testing the model, its accuracy drops substantially, showing the importance of these intermediate tokens.
Related Work
Let’s Think Dot by Dot: Hidden Computation in Transformer Language Models[1] is a recent paper that also explores the use of blank tokens between the input and output to enhance the computational abilities of a transformer model. They find that this approach is very effective for some simple algorithmic problems, although it appears to have fundamental theoretical limitations. Specifically, they argue that blank tokens are only expected to enhance performance in tasks that can be decomposed into parallel sub-problems. It would be interesting to investigate whether the list sorting algorithm learned by the above model has a parallel structure, or whether it has been able to perform serial computation within the blank tokens.
Future Implications
Models like this show an exciting possible future for machine learning, where transformers can learn efficient multi-step solutions to complex problems by themselves. That being said, this investigation was very primitive, and leaves a lot of open questions:
- How far does this method scale? Can the theoretical limitations found by Pfau et al.[1] be overcome to tackle more complex problems like graph search or game playing?
- Can the length of the reasoning trace be varied based on the problem complexity? The current model always outputs the same number of blank tokens, even though shorter and simpler lists shouldn’t need as many. Can we train the model to stop and output the answer as soon as it has had enough time?
- Are there difficult problems where a transformer model could learn more efficient algorithms without being tied to the limitations of human language?
- The above model often gets stuck in local minima during training, so several training attempts are required before it converges successfully. Why does this happen, and can it be made more reliable?
- Can a system like this be connected to a large language model to allow natural language interaction with the reasoning process?
If methods like the above can be scaled up successfully, we could see transformer models that continually take in data and perform sophisticated internal calculations to quickly produce solutions to the world’s most difficult problems. I’m hoping to try this method on more challenging algorithmic problems, to discover and expand the limits of this approach.
References
[1] Pfau, Jacob, William Merrill, and Samuel R. Bowman. “Let’s Think Dot by Dot: Hidden Computation in Transformer Language Models.” arXiv preprint arXiv:2404.15758 (2024). https://arxiv.org/abs/2404.15758.